sandbox/M1EMN/Exemples/maree_bretagne.c
Marées proche Atlantique, Manche et bas de la Mer du Nord
Knowing the tide and the currents is of the uttermost importance for sailors. In Brittany (Bretagne), in the channel (la Manche), the currents are almost the strongest in the world, and the tide amplitude as well. To avoid shipwrecks, every captain has a nautical almanach like “Annuaire du Marin Breton” and the SHOM table of the tide currents on board.
Relation between moon and sun movment has been long recognized (since Pythéas from Marseille voyage of exploration to northwestern Europe in -325)…
….bla bla …. Marée statique de Newton … \gamma(M)-\gamma(0)=\frac{2 G M_LR}{D^3}=2 \frac{G M_T}{R^2}\frac{M_L R^3}{M_T D^3}…. Poincaré “Marée du Baccalauréat” (cf Bouteloup) ….bla bla ….
Laplace extended this theory to compute the tides from observations….bla bla ….
A tide analog computer has been constructed by Kelvin (link to a photo to come from Arts & Métiers Réserve) to forcast the tides.
….bla bla ….
Here we propose a numerical implementation of a temptative to compute tides around France based on Tsunami example. Only M2 wave is given (only Moon contribution) at the left of the domain in Atlantic ocean the first of August 2017 (time in TU+1). It needs 3 days to obtain the forced state which is compared to the values of the M2 contibution from “Table des Marées des grands Ports du Monde”.
Solver setup
The following headers specify that we use the Saint-Venant solver together with (dynamic) terrain reconstruction and an adaptation of adapt_wavelet_limited.h
#include "spherical.h"
#include "saint-venant.h"
#include "terrain.h"
#include "adapt_wavelet_limited.h"We then define a few useful macros and constants.
#define ETAE 1e-2 // error on free surface elevation (1 cm)
#define HMAXE 5e-2 // error on maximum free surface elevation (5 cm)
int MAXLEVEL,MINLEVEL;
double z0=0.,tmax;
int baz=0;When using a quadtree (i.e. adaptive) discretisation, we want to start with the coarsest grid, otherwise we directly refine to the maximum level. Note that 1 << n is C for 2^n.
int main()
{https://www.ngdc.noaa.gov/mgg/global/etopo2.html resolution of ETOPO2v2: The horizontal grid spacing is 2-minutes of latitude and longitude (1 minute of latitude = 1.853 km at the Equator). The vertical precision is 1 meter.
as the domain is 10 degrees=600NM hence 1111km
MAXLEVEL=7; 2^7=128 gives detail of size 8.7 km=4.4NM
MAXLEVEL=9; 2^9=512 gives detail of size 2.2 km=1.2NM
MAXLEVEL=10; 2^{11}=2048 gives detail of size 1.08 km=0.6NM
—change the value: the domain is now 12.5
// FILE *fichier = fopen("/Users/pyl/basilisk/test_pyl/Tsunami/WORD/etopo2.kdt", "r");
// if (fichier == NULL){baz=1;}else{baz=0;};
if(access("/Users/pyl/basilisk/test_pyl/Tsunami/WORD/etopo2.kdt",F_OK)==0) {
fprintf(stderr,"local!\n");
MAXLEVEL=8; //9 //
MINLEVEL=7;
baz=0;
} else {
fprintf(stderr,"on basilisk's server !\n");
MAXLEVEL=7;
MINLEVEL=6;
baz=1;
}
fprintf(stderr,"%d \n",baz);
#if QUADTREE
// grid points to start with
N = 1 << MINLEVEL;
#else // Cartesian
// grid points
N = 1 << MAXLEVEL;
#endifHere we setup the domain geometry. For the moment Basilisk only supports square domains. For this example we have to use degrees as horizontal units because that is what the topographic database uses (eventually coordinate mappings will give more flexibility). We set the size of the box L0 and the coordinates of the lower-left corner (X0,Y0). The domain is 10 degrees squared
Radius = 6371220.;
L0 = 12.5;
// use L0=25 to catch Gibraltar and south of Norway and Shetland
// centered on 48 longitude,latitude -2
X0 = -2 - L0/2.;
Y0 = 48. - L0/2.;G is the acceleration of gravity required by the Saint-Venant solver. This is the only dimensional parameter. We rescale it so that time is in minutes, horizontal distances in degrees and vertical distances in metres.
Acceleration of gravity is in (degrees^2)/(min^2)/m
This is a trick to circumvent the current lack of coordinate mapping.
units : meters in z but degrees en x,y, so 60 Miles 40075e3/360.= 111.111km which is 60 times one Nauticale Miles 1852m.
G=9.81*sq(60.);
// time in minutes, one day 24*60min computation during half a week
tmax=24*60*3.5;
//tmax=1000;We then call the run() method of the Saint-Venant solver to perform the integration.
run();
}We declare and allocate another scalar field which will be used to store the maximum wave elevation reached over time.
scalar hmax[];Boundary conditions
We set the normal velocity component on the left, right and bottom boundaries to a “radiation condition” with a reference sealevel of zero. see http://basilisk.fr/src/elevation.h#radiation-boundary-conditions
The bottom boundary is always “dry” in this example so can be left alone. Note that the sign is important and needs to reflect the orientation of the boundary. At first we just put the period of M2 tide of the Moon (a complete computation needs the Sun AS2 and all the harmonics…) The period of M2 is 12.4206h = 12h24min14s (745.236 minutes, 44714.2 s).
the amplitude 2.00 and phase shift 320 of the velocity at the entrance of the domain are adjusted to fit the M2 tide as soon as possible after the first of August 2017 (this is a trick).
u.n[right] = + radiation(z0);
u.n[bottom] = - radiation(z0);
u.n[top] = + radiation(z0);
u.n[left] = - radiation(z0+2.39*sin(2*pi*(t+320-30)/(745.236)));Adaptation
Here we define an auxilliary function which we will use several times in what follows. Again we have two #if…#else branches selecting whether the simulation is being run on an (adaptive) quadtree or a (static) Cartesian grid.
We want to adapt according to two criteria: an estimate of the error on the free surface position – to track the wave in time – and an estimate of the error on the maximum wave height hmax – to make sure that the final maximum wave height field is properly resolved.
We first define a temporary field (in the automatic variable η) which we set to h+z_b but only for “wet” cells. If we used h+z_b everywhere (i.e. the default \eta provided by the Saint-Venant solver) we would also refine the dry topography, which is not useful.
adapt_wavelet_limited.h is used here, thanks to Cesar Pairetti, but as Stephane says: “Ideally, automatic adaptation using only error control (i.e. cmax in adapt_wavelet) should be more reliable and less susceptible to”user error“. I know of many examples where the adaptation functions in Gerris have been abused in this way, leading to erroneous simulations. So, hand-tuning should only be used as a last resort.”
Set max refinement level inside circle, maximum refinement everywhere else
int maXlevel(double x,double y, double z){
int lev;
if(sqrt(sq(x+2.5)+sq(y-48.6))< .2)
lev = MAXLEVEL+2;
else
lev = MAXLEVEL;
return lev;
}
int adapt() {
#if QUADTREE
scalar eta[];
foreach()
eta[] = h[] > dry ? h[] + zb[] : z0;
boundary ({eta});We can now use wavelet adaptation on the list of scalars {η,hmax} with thresholds {ETAE,HMAXE}. The compiler is not clever enough yet and needs to be told explicitly that this is a list of doubles, hence the (double[]) type casting. The function then returns the number of cells refined.
astats s = adapt_wavelet_limited ({eta, hmax}, (double[]){ETAE,HMAXE}, maXlevel, MINLEVEL);
// astats s = adapt_wavelet ({eta, hmax}, (double[]){ETAE,HMAXE}, MAXLEVEL, MINLEVEL);
// fprintf (stderr, "# refined %d cells, coarsened %d cells\n", s.nf, s.nc);
return s.nf;
#else // Cartesian
return 0;
#endif
}Initial conditions
We first specify the terrain database to use to reconstruct the topography z_b. This KDT database needs to be built beforehand. See the xyz2kdt manual for explanations on how to do this.
The next line tells the Saint-Venant solver to conserve water surface elevation rather than volume when adapting the mesh.
event init (i = 0)
{
if(access("/Users/pyl/basilisk/test_pyl/Tsunami/WORD/etopo2.kdt",F_OK)==0) {
fprintf(stderr,"Le fichier existe !\n");
terrain (zb, "/Users/pyl/basilisk/test_pyl/Tsunami/WORD/etopo2", NULL); // topo is somewhere in my HD
baz=0;
} else {
fprintf(stderr,"Le fichier n'existe pas !\n");
terrain (zb, "/home/basilisk/terrain/etopo2", NULL); // topo is on baz's server!
baz=1;
}
// Glurps there is stil a bug there?????
conserve_elevation();The initial still water surface is at z=0 so that the water depth h is…
At each timestep
We use a simple implicit scheme to implement quadratic bottom friction i.e. \displaystyle \frac{\partial \mathbf{u}}{\partial t} = - C_f|\mathbf{u}|\frac{\mathbf{u}}{h} with C_f=10^{-3}.
event friction (i++) {
double Cf=10e-4;
foreach() {
double a = h[] < dry ? HUGE : 1. + Cf*dt*norm(u)/(h[]);
foreach_dimension()
u.x[] /= a;That is also where we update hmax.
if (h[] > dry && h[] + zb[] > hmax[])
hmax[] = h[] + zb[];
}
boundary ({hmax, u});
}Add now we compute the Coriolis force (time unit : minute) \displaystyle \frac{\partial \mathbf{u}}{\partial t} = -2 \omega \sin \lambda \times \mathbf{u} with \lambda around 48° (this is y ), and sideral period 23h56min 04s = 1436.07 min.
The splited derivative is solved in a implicit way: \displaystyle \frac{\partial u}{\partial t} = 2 \omega \sin \lambda v, \;\; \;\; \frac{\partial v}{\partial t} = -2 \omega \sin \lambda u define \Omega = 2 \omega \sin \lambda, write Z=u+iv so \frac{\partial Z}{\partial t} = -i \Omega Z so \displaystyle Z^{n+1}= \frac{Z^{n}}{1+ i \Omega \Delta t} which gives \displaystyle u^{n+1} = \frac{u^n+(\Omega \Delta t) v^n}{1 + (\Omega \Delta t)^2)},\;\; v^{n+1} = \frac{v^n -(\Omega \Delta t) u^n }{1 + (\Omega \Delta t)^2)}
event coriolis (i++) {
double Omeg,Ro,u1,v1;
foreach() {
Omeg=2*sin(y*pi/180.)*(2*pi/1436.07);
Ro=1 + sq(Omeg*dt);
u1=(u.x[] + u.y[]*(Omeg*dt))/Ro;
v1=(u.y[] - u.x[]*(Omeg*dt))/Ro;
u.x[]=u1;
u.y[]=v1;
}
boundary ({u.x,u.y});
}Movies
This is done every minute (t++). The static variable fp is NULL when the simulation starts and is kept between calls (that is what static means). The first time the event is called we set fp to a ppm2mpeg pipe. This will convert the stream of PPM images into an mpeg video using ffmpeg externally.
We use the mask option of output_ppm() to mask out the dry topography. Any part of the image for which m[] is negative (i.e. for which etam[] < zb[]) will be masked out.
event movies (t+=10) {
// static FILE * fp = popen ("ppm2mpeg > eta.mpg", "w");
scalar m[], etam[];
foreach() {
etam[] = eta[]*(h[] > dry);
m[] = etam[] - zb[];
}
boundary ({m, etam});save only the last period in a film (play the film in loop!), and save one image to display
// if(t>(tmax - 745.236))
output_ppm (etam, file = "eta.mp4", mask = m,min = -3, max = 3, n = 1024, linear = true);
if(t==2500) {
output_ppm (etam, file = "eta.png", mask = m,min = -5, max = 5, n = 512, linear = true);
output_ppm (hmax, file = "hmax.png", mask = m,min = -5, max = 5, n = 512, linear = true);
}We also use the box option to only output a subset of the domain (defined by the lower-left, upper-right coordinates).
//static FILE * fp2 = popen ("ppm2mpeg > eta-zoom.mpg", "w");
//output_ppm (etam, fp2 , mask = m, min = -3 , max = 3, n = 1024, linear = true,box = {{-4.8,48},{2.,51.3}});
output_ppm (etam, file ="eta-zoom.mp4", mask = m, min = -3 , max = 3, n = 1024, linear = true,box = {{-4.8,48},{2.,51.3}});
//if((t>=tmax-2*745.236)&&(t<tmax))
//{output_ppm (etam, file ="eta-SM.mp4", min = -3 , max = 3, n = 1024, linear = true,box = {{-4.14,48.46},{1.23,49.8}}); }
if(t>0)
output_ppm (etam, file ="eta-SM.mp4", min = -5 , max = 5, n = 1024, linear = true, box = {{-3.4,48.5},{-1.5,50}});
if(t>0)
output_ppm (etam, file ="eta-22.mp4", min = -4 , max = 4, n = 512, linear = true, box = {{-2.68333,48.4833},{-2.271388,48.7}});
//if(sqrt(sq(x+2.5)+sq(y+48.6))< .2)
// from
// 48°29'24.3"N 2°40'59.6"W
// to
// 48°42'02.4"N 2°16'17.1"W
if(t==1000) {
output_ppm (etam, file = "eta-zoom.png", mask = m,min = -3, max = 3, n = 256, linear = true,box = {{-4.8,48},{2.,51.3}});
}And repeat the operation for the level of refinement…
// static FILE * fp1 = popen ("ppm2mpeg > level.mpg", "w");
scalar l = etam;
foreach()
l[] = level;
output_ppm (l, file="level.mp4", min = MINLEVEL, max = MAXLEVEL+2, n = 512);
if(t==1000) {
output_ppm (l, file = "level.png", mask = m, min = MINLEVEL, max = MAXLEVEL+2, n = 512, linear = true);
}
foreach()
l[] = level;
boundary ({l});
output_ppm (l, n = 512, min = MINLEVEL, max= MAXLEVEL+2,
// box = {{0,-1},{10,2.5}},
file = "level.mp4") ;…and for the process id for parallel runs.
Tide gauges
We define a list of file names, locations and descriptions and use the output_gauges() function to output timeseries (for each timestep) of \eta for each location.
Gauge gauges[] = {
// file lon lat description
{"manche.txt", 0, 50, "#dans la manche"},
{"saintmalo.txt", -2.140962, 49, "#SM"},
{"rotterdam.txt", 4.095950 , 52.092836, "#Rott"},
{"brest.txt", -4.806819, 48.214563, "#Brst"},
{"houat.txt", -2.708353,47.406863,"#Houat"},
{"large.txt", -6.5, 48, "#large"},
{NULL}
};
event gauges1 (t += 15; t <= tmax) output_gauges (gauges, {eta});Adaptivity
And finally we apply our adapt() function at every timestep.
event do_adapt (i++) adapt();Run
compilation
qcc -g -O2 marees_bretagne.c -o marees_bretagne ~/basilisk-darcs/src/kdt/kdt.o -lm
./marees_bretagne make maree_bretagne.tst;make maree_bretagne/plots;make maree_bretagne.c.htmlResults: images, movies
After completion this will give the following images and animations:
Maximum elevation of tide, note that Saint Malo and Bristol bay are indeed high tide places. Note the green spot (hum, hard to see) corresponing to the amphidromic points north of France.
The animation of the full domain:
Animation of the full domain
A zoom in “La Manche”
Animation of the wave elevation. Dark blue is -2 metres and less. Dark red is +2 metres and more.
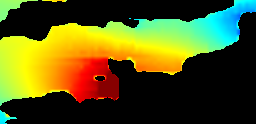
Animation of the wave elevation. Dark blue is -2 metres and less. Dark red is +2 metres and more.
Animation of the wave elevation Saint Malo
Animation of a very special place!
adaptation level
Animation of the level of refinement. Dark blue is 7 (128 pt 4.4NM/cel) and dark red is 9 (512 pt, precision 3M/cel )
Results tides
From “Table des Marées des Grands Ports du Monde”, SHOM 1984, the sun and moon contribution are: \displaystyle \frac{\text{Z0}}{100} + \frac{\text{AM2} \cos \left(\frac{1}{180} \pi \left(-\text{GM2}+2 \left(\text{h0}+\left(\frac{\text{heure}}{24}+13270\right) \text{hp0}\right)-2 \left(\left(\frac{\text{heure}}{24}+13270\right) \text{sp0}+\text{s0}\right)+30 \text{heure}\right)\right)+\text{AS2} \cos \left(\frac{1}{180} \pi (30 \text{heure}-\text{GS2})\right)}{1000} with the parameters for Brest \displaystyle \{\text{Z0}\to 445,\text{AM2}\to 2160,\text{GM2}\to 142,\text{AS2}\to 755,\text{GS2}\to 182\} and astronomical parameters \displaystyle \{\text{s0}\to 78.16,\text{sp0}\to 13.1764,\text{h0}\to 279.82,\text{hp0}\to 0.985647\}
So that the value of the tide in Brest from the SHOM table the 1st of August 2017 (time in TU+1) is \displaystyle Z(t)= Z_0 + AS_2 \cos(GS_2- WS_2 t) + AM_2 \cos(GM_2 - WM_2 t) with Moon parameters amplitude AM_2=2.16, phase GM_2=5642.320805440571, period WM_2=0.5058680493365497/60 which is 12h25min14s (low tide to hight tide 6h12m37s) 44714.1643s (745.2360 min)
and sun parameters WS_2=0.5235987755982988/60 which is 12 hours, (low tide to hight tide 6h) AS_2 =0.755m the amplitude GS_2 = 3.1764992386296798 the phase shift
and mean height Z_0=4.45m
here we just plot the tide from SHOM, it shows the influence of sun
set xlabel "t in min"
set ylabel "h in m"
Z0=4.45
AM2=2.16
AS2 =0.755
h1(x)=AS2*cos(3.1764992386296798 - 0.5235987755982988*x/60)
h2(x)=AM2*cos(5642.320805440571 - 0.5058680493365497*x/60)
p[0:24*60]Z0+h1(x)+h2(x) t'maree Brest SHOM 2 modes' w l, Z0+h2(x) t'onde M2 uniq.'
maree a Brest deux premiers modes le 1er Aout 2017 pendant un jour (script)
Plot of the tide in Brest and height at the boundary condition, the phase shift and amplitude of the left BC have been adjusted to fit more or less the tide in Brest
set xlabel "t in min"
set ylabel "h in m"
p[0:]'large.txt' w lp,'brest.txt' w lp, h2(x) t'onde M2 uniq.'
au large (condition d’entree) (script)
Once, the phase shift and amplitude of the left BC have been adjusted in radiation BC, we check that the computed M2 tide in Saint Malo is not so far from the SHOM the 1st of August 2017 \displaystyle Z(t)= Z_0 +
AM_2 \cos(GS_2 - WM_2 t) Z_0=6.71 m with Moon parameters amplitude AM_2=3.68, phase is GS_2=5643.47, period WM_2=0.5058680493365497/60
(we remove the Z_0 in the plot as we start by a mean constant level which takes into account the initial depth in the tiopography)
set xlabel "t in min"
set ylabel "h in m"
sm2(x)= 3.68*cos(5643.47 - 0.505868*x/60)
p[0:][:7]'brest.txt' w lp, h2(x) t' Brest onde M2 uniq.','saintmalo.txt' w lp,sm2(x) t' SM onde M2 uniq.'
Brest calculé et Brest SHOM et Saint Malo Calculé et Saint Malo SHOM (script)
The Saint Malo is underpredicted, the tides are not synchronized with Brest as there is propagation in the channel. Removing rotation decreases SM tide.
set xlabel "t in min"
set ylabel "h in m"
sm2(x)= 3.68*cos(5643.47 - 0.505868*x/60)
p[64*60:24*3.5*60][:7]'brest.txt' w lp, h2(x) t' Brest onde M2','saintmalo.txt' w lp,sm2(x) t'SM onde M2'
Brest calculé et Brest SHOM et Saint Malo Calculé et Saint Malo SHOM (script)
Plot of tide in several harbours (with ‘rotterdam.txt’, which has to be checked); note amplification in Saint Malo, but little bit too small compared to reality. Houat is in phase with Brest as expected (amplitude should be smaller).
set key left
set xlabel "t in min (1day=1440min)"
set ylabel "h in m"
p[2000:5000][:8]'saintmalo.txt' w lp,sm2(x) t'SM M2','brest.txt' w lp,h2(x) t'B M2','houat.txt' w l,'manche.txt' w l,'rotterdam.txt'
(script)
Links
- inspired/plagied from tsunami 2004
- see http://basilisk.fr/src/examples/tides.c
- http://gerris.dalembert.upmc.fr/gerris/examples/examples/tides.html
- Gerris/modules/fes2004/
bibliography
- cours PYL
- Phan et a. Méthodologie pour la simulation de la marée avec la version 6.2 de TELEMAC- 2D et TELEMAC-3D
- SHOM Table des Marées des grands ports du Monde 1984
- “Tout savoir sur les marées” Odile Guérin/ Ouest-France/ 2004
- “La marée” B. Simon & A. Lahaye-Collomb, Les guides du SHOM 1997
- La Marée (941-MOG), Les Guides du SHOM
- Trois cents ans de mesures marégraphiques en France : (…) port de Brest, N. Pouvreau
- PYL copie perso de “table des marées des grands ports du monde” du SHOM (1984) tabledesmareesdesgrandsportsdumonde.pdf
- Jacques Bouteloup “Vagues, marées, courants marins” Que sais-je, 1979
notes
bug de formule en local sous macosx
make maree_bretagne/plots;make maree_bretagne.c.html
sed -i -e 's/\\)//g' maree_bretagne.c.html;sed -i -e 's/\\(//g' maree_bretagne.c.html
sed -i -e 's/\\\[//g' maree_bretagne.c.html
sed -i -e 's/\\\]//g' maree_bretagne.c.html;the simple HTML tag works as well:
lien tout bête
un autre:
lien tout bête
