Non_dimensionalization

Non-dimensionalisation
Basilisk numerical resolution of the momentum equation of Navier-Stokes

Non-dimensionalisation

The system studied, is the motion of a droplet by Marangoni effect in a linear gradient of surface tension.

Input : linear surface tension field \displaystyle \gamma(x) = G_\gamma . x + \gamma_0
Output : velocity of the droplet

Navier-Stokes equations for incompressible fluids

We have the three following conservation laws (mass, momentum and energy)

\displaystyle div(\vec{u}) = 0 \displaystyle \rho \frac{d\vec{u}}{dt} = -\vec{\nabla} p + \mu \Delta \vec{u} + \rho \vec{g} + (\gamma \kappa \vec{n} + \vec{\nabla}_s \gamma) \delta_s \displaystyle \frac{\partial}{\partial t} \left( \frac{1}{2} \rho \mid{u}\mid^2 + \rho e \right) + \vec{\nabla} . \left( \left(\frac{1}{2} \rho \mid{u}\mid^2 + \rho e \right) \vec{u} \right)-\vec{\nabla} . \left( \overline{\overline{\sigma}} . \vec{u} \right) - \lambda \Delta T = \rho \vec{f} . \vec{u} + Q

with :

\rho [kg/m^3] : the fluid’s mass density ;
\vec{u} [m/s] : the fluid’s velocity ;
p [kg.m/s^2)] : the fluid’s pressure ;
\mu [kg/(m.s)] : the fluid’s dynamic shear viscosity ;
g [m/s^2] : the standard gravity ;
\gamma [J/m^2] : the superficial tension between the two fluids ;
G_\gamma [J/m^3] : the superficial tension spatial gradient ;
\kappa [m^{-1}] : the surface curvature ;
\delta_s [1] : the delta function which insures the surface tension \gamma is only on the interface ;
\vec{n} : the normal vector to the interface
e [J/kg] : the system’s density of internal energy ;
\lambda [W/(m.°C)] : the fluid’s thermal conductivity ;
T [°C] : the temperature ;
\overline{\overline{\sigma}} [kg/(m.s^2)] : the symetrical interior shear tensor ;
\vec{f} [kg/(m.s)^2] : the external force density ;
Q [W/m^3] : the inflow of thermal energy.

First we have to determine the characteristic unit of measure to non-dimentionalize the Navier-Stokes equations.

Non-dimentional numbers

Reynolds number : Re = \frac{F_{inertial}}{F_{viscous}} = \frac{\rho . X . u}{\mu}
Capillarity number : Ca = \frac{F_{viscous}}{\gamma} = \frac{u . \mu}{\gamma}

with : \rho [kg/m^3] the mass density of the fluid, X [m] the typical length of our system, u [m/s] the typical velocity of the fluid, \mu the fluid’s dynamical shear viscosity.

Characteristic unit of measure

The units are : m [kg], l [m] and t [s].

l_c = R_c
m_c = \rho_c . R_c^3
$t_c = = $ the viscuous diffusion time.

The characteristic values that allow to non-dimensionalize the equations are : R_c, \rho_c, \mu_c

Variables non-dimensionalization

For the momentum conservation law, we get :

\rho . \frac{d \vec{u}}{dt} = - \nabla p + \mu \Delta \vec{u} + \rho \vec{g} + (\gamma \kappa \vec{n} + \vec{\nabla}_s \gamma )\delta_s

\Leftrightarrow \frac{d \vec{u}}{dt} = - \frac{1}{\rho} \nabla p + \frac{\mu}{\rho} \Delta \vec{u} + \vec{g} + (\frac{\gamma}{\rho} \kappa \vec{n} + \frac{1}{\rho} . \vec{\nabla}_s \gamma )\delta_s

\Leftrightarrow \frac{u_c^2}{R_c}\frac{d \vec{u}^*}{dt^*} = - \frac{u_c^2}{ \rho^* . R_c} \nabla^* p^* + \frac{\mu_c . \mu^* . u_c}{\rho_c . \rho^* . R_c^2} \Delta^* \vec{u}^* + \frac{u_c^2}{R_c}\vec{g}^* + (\frac{\gamma_c . \gamma^*}{\rho_c . \rho^* . {R_c}} \kappa^* \vec{n} + \frac{\gamma_c}{\rho_c . \rho^* . R_c} . \vec{\nabla}^*_s \gamma^* )\frac{\delta_s^*}{R_c}

\Leftrightarrow \frac{d \vec{u}^*}{dt^*} = - \frac{p_c }{\rho_c . \rho^* . u_c^2} \nabla^* p^* + \frac{\mu_c . \mu^* }{\rho_c . \rho^* . u_c . R_c} \Delta^* \vec{u}^* + \vec{g}^* + (\frac{\gamma_c . \gamma^*}{\rho_c . \rho^* . {u_c^2}} \kappa^* \vec{n} + \frac{\gamma_c}{\rho_c . \rho^* . u_c^2} . \vec{\nabla}^*_s \gamma^* )\frac{\delta_s^*}{R_c}

\Leftrightarrow \frac{d \vec{u}^*}{dt^*} = - \frac{1}{\rho^*} \nabla^* p^* + \frac{\mu^* }{\rho^*} \frac{1}{Re_c} \Delta^* \vec{u}^* + \vec{g}^* + \frac{1}{Re_c . Ca_c}(\frac{\gamma^*}{\rho^*} \kappa^* \vec{n} + \frac{1}{ \rho^* } . \vec{\nabla}^*_s \gamma^* )\delta_s^*

With : \vec{\nabla}_s \gamma = \vec{\nabla}\gamma - \left( \vec{\nabla}\gamma \vec{n} \right) \vec{n} \right) \right)

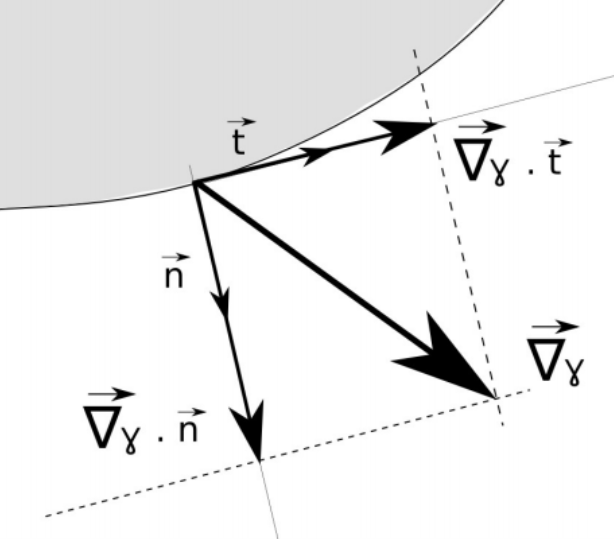
Decomposition of the tangential component of the gradient

Momentum equation non-dimentionalized

\displaystyle \frac{d \vec{u}^*}{dt^*} = - \frac{1}{\rho^*} \nabla^* p^* + \frac{\mu^* }{\rho^*} \frac{1}{Re_c} \Delta^* \vec{u}^* + \vec{g}^* + \frac{1}{Re_c . Ca_c} \left( \frac{\gamma^*}{\rho^*} \kappa^* \vec{n} + \frac{1}{ \rho^* } \left( \vec{\nabla}^*\gamma^* - \left( \vec{\nabla}^*\gamma^* \vec{n} \right) \vec{n} \right) \right) \delta_s^*

Parameters of the equation

Re_c = \frac{\rho_c . R_c . u_c}{\mu_c} and Ca_c = \frac{u_c . \mu_c}{\gamma_c}

There is no typical velocity that characterizes our problem. Therefore, we define a characteristic velocity u_c based on the input, which is the gradient of surface tension.

Ca_c = \frac{\mu_c . u_c}{\gamma_c} and G^*_\gamma = \frac{G_\gamma . R_c}{\gamma_c}

Ca_c = G^*_\gamma \Leftrightarrow \frac{G_\gamma . R_c}{\gamma_c} = \frac{\mu_c . u_c}{\gamma_c}

\displaystyle u_c = \frac{G_\gamma . R_c}{\mu_c}

Finally :

Re_c = \frac{\rho_c . R^2_c . G_\gamma}{\mu^2_c}
Ca_c = \frac{G_\gamma . R_c}{\gamma_c}

Basilisk numerical resolution of the momentum equation of Navier-Stokes

We solve only one equation for two fluids. This is possible thanks to the VOF (Volume of fluid) method.

Mass density and dynamical vicosity

\rho(c) = c . \rho_c + (1-c) \lambda_\rho . \rho_c
\mu(c) = c . \mu_c + (1-c) \lambda_\mu . \mu_c

Surface tension

\gamma(x) = G_\gamma . x + \gamma_0

Hypotheses

No pressure
No gravity

Momentum equation non-dimentionalized

\displaystyle \frac{d \vec{u}^*}{dt^*} = \frac{\mu^{**}}{\rho^*} \Delta^* \vec{u}^* + \left( \frac{\gamma^{**}}{\rho^*} \kappa^* \vec{n} + \frac{1}{ \rho^* } \left( \vec{\nabla}^*\gamma^{**}-\left( \vec{\nabla}^*\gamma^{**} \vec{n} \right) \vec{n} \right) \right) \delta_s^*

with : \gamma^{**} = \frac{\gamma^*}{Re_c . Ca_c} and \mu^{**} = \frac{\mu^*}{Re_c}