initial_conditions_dimonte_fft2.h

Initializing an interface using a given spectrum
References

Initializing an interface using a given spectrum

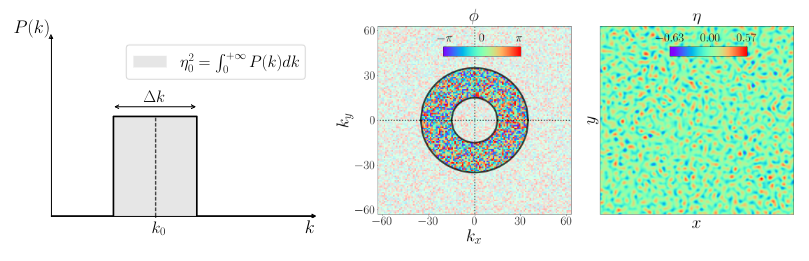
Consider \eta(x, y) being a zero mean, periodic initial perturbation at the interface between two fluids. This perturbation is further characterized by the horizontal discrete Fourier modes \hat{\eta} of wavevector \vec{k} = (k_x, k_y)^T \in \mathbb{Z}^2 and modulus k = \vert\vert k \vert\vert such that

\displaystyle \eta(x,y) = \sum \hat{\eta}(\vec{k}) e^{i(k_x x + k_y y)}

The realizability condition, \eta \in \mathbb{R}, imposes that for the complex Fourier modes \hat{\eta}(-\vec{k}) = \hat{\eta}^*(\vec{k}).

We further consider an annular spectrum for the interface perturbation as in Dimonte et al. (2004) of the form

\displaystyle \hat{\eta}(\vec{k}) = e^{i\phi(\vec{k})} \times \begin{cases} cst/k & \text{ for } \vert\vert k - k_0 \vert\vert \leq \Delta k/2 \\ 0 & \text{otherwise} \end{cases}

with

k_0 being the mean wavenumber
\Delta k the bandwidth of the perturbation
\phi the phase of the modes (here is randomly sampled)
\eta_0 the rms amplitude

An example of the initialized interface using isvof=0 (left) and isvof=1 (right).

To initialize the interface we’ll use a Fourier transform and some interpolation routines from GSL.

#include <gsl/gsl_fft_complex.h>
#include <gsl/gsl_complex.h>
#include <gsl/gsl_complex_math.h>
#include <gsl/gsl_interp2d.h>
#include <gsl/gsl_spline2d.h>
#pragma autolink -lgsl -lgslcblas
#define REAL(z,i) ((z)[2*(i)])
#define IMAG(z,i) ((z)[2*(i)+1])

Save the initial perturbation in a gnuplot-compatible format

save_data_for_gnuplot_complex(): saves a (complex) 2D array as a .dat file

void save_data_for_gnuplot_complex(double *data, int NX, const char *filename){
  FILE *file = fopen(filename, "w");
  if (file == NULL){
    fprintf(stderr, "Error opening file %s\n", filename);
    return;
  }

  for (int i = 0; i < NX; i++){
    for (int j = 0; j < NX; j++){
      int index = i * NX + j;
      double magnitude = sqrt(sq(REAL(data, index)) + sq(IMAG(data, index)));
      fprintf(file, "%d %d %f %f %f\n", i, j, REAL(data,index), IMAG(data,index), magnitude);
    }
    fprintf(file, "\n"); 
  }
  fclose(file);
}

save_data_for_gnuplot_real(): saves a 2D array as a .dat file

void save_data_for_gnuplot_real(double *data, int NX, const char *filename){
  FILE *file = fopen(filename, "w");
  if (file == NULL){
    fprintf(stderr, "Error opening file %s\n", filename);
    return;
  }

  for (int i = 0; i < NX; i++){
    for (int j = 0; j < NX; j++){
      int index = i * NX + j;
      fprintf(file, "%d %d %f \n", i, j, data[index]);
    }
    fprintf(file, "\n"); 
  }
  fclose(file);
}

Generate the perturbation in Fourier space and return to physical space

init_2D_complex(): initializes the perturbation in Fourier space

void init_2D_complex(double *data, int n0, int n1, double kmin, double kmax, double eta0_target=1){
  double *kx = malloc(n0 * sizeof(double));
  double *ky = malloc(n1 * sizeof(double));
  double cst = eta0_target / sqrt((2*pi*log(kmax/kmin)));

Calculate horizontal wavenumbers

  for (int i = 0; i <= n0 / 2; ++i)
    kx[i] = 2 * pi * i / L0;

  for (int i = n0 / 2 + 1; i < n0; ++i)
    kx[i] = 2 * pi * (i - n0) / L0;

  for (int i = 0; i <= n1 / 2; ++i)
    ky[i] = 2 * pi * i / L0;

  for (int i = n1 / 2 + 1; i < n1; ++i)
    ky[i] = 2 * pi * (i - n1) / L0;

Initialize spectrum in the annular region with magnitude cst/k and random phase

  double dkx = kx[1]-kx[0];
  double dky = ky[1]-ky[0];
  double eta0 = 0.;
  memset(data, 0, 2 * n0 * n1 * sizeof(double));
  for (int i = 0; i < n0; ++i){
    for (int j = 0; j < n1; ++j){
      double k = sqrt(sq(kx[i]) + sq(ky[j]));
      if ((k >= kmin) && (k < kmax)){
        double magnitude = cst / k;
        double phase = noise() * pi;
        REAL(data, i*n1+j) = magnitude * cos(phase);
        IMAG(data, i*n1+j) = magnitude * sin(phase);
        eta0 += sq(magnitude)*dkx*dky;
      }
    }
  }

  fprintf(stdout, "real eta0 is %g \n", sqrt(eta0));

  free(kx);
  free(ky);
}

fft2D(): uses the radix-2 routines to return to physical space

void fft2D(double *data, int n0, int n1){  
  
  // FFT along rows 
  for (int i = 0; i < n0; ++i){
    gsl_fft_complex_radix2_forward(data + 2 * i * n1, 1, n1);
  }

  // FFT along columns
  double *column = malloc(2 * n0 * sizeof(double));
  for (int j = 0; j < n1; ++j){
    for (int i = 0; i < n0; ++i){
      REAL(column,i) = REAL(data, i*n1 + j);
      IMAG(column,i) = IMAG(data, i*n1 + j);
    }
    gsl_fft_complex_radix2_forward(column, 1, n0);
    for (int i = 0; i < n0; ++i)
    {
      REAL(data, i*n1 + j) = REAL(column,i);
      IMAG(data, i*n1 + j) = IMAG(column,i);
    }
  }
  free(column);
}

Apply the initial condition to a scalar field

initial_condition_dimonte_fft2(): Initializes a scalar field with a perturbation

This function initializes a scalar field phi with a perturbation generated using a 2D Fast Fourier Transform (FFT). The perturbation is generated by the main process and broadcasted to other processes if MPI is used. The perturbation can be applied directly to the field or used to generate a Volume of Fluid (VOF) surface.

The arguments and their default values are:

phi: vertex scalar field to be initialized.
amplitude: amplitude of the perturbation. Default is 1.
NX: number of points along the x-dimension. Default is N.
NY: number of points along the y-dimension. Default is N.
kmin: minimum wavenumber for the perturbation. Default is 1.
kmax: maximum wavenumber for the perturbation. Default is 1.
isvof: flag to indicate if the perturbation is applied directly to the field (isvof=0) or used to generate a VOF surface (isvof=1). Default is 0.

Example Usage

initial_condition_dimonte_fft2(phi, 0.5, 128, 128, 0.1, 10.0, true);

see, also example 1, example 2 and example 3

void initial_condition_dimonte_fft2(vertex scalar phi, double amplitude=1, int NX=N, int NY=N, double kmin=1, double kmax=1, bool isvof=0){
  
  // We declare the arrays and initialize the physical space
  double *data = malloc(2 * NX * NY * sizeof(double));
  double *xdata = (double *)malloc(NX * sizeof(double));
  double *ydata = (double *)malloc(NY * sizeof(double));
  double *zdata = (double *)malloc(NX * NY * sizeof(double));

  double dx = L0 / (NX - 2);
  for (int i = 0; i < NX; i++){
    xdata[i] = i * dx + X0;
  }

  double dy = L0 / (NY - 2);
  for (int j = 0; j < NY; j++){    
    ydata[j] = j * dy + Y0;
  }

  // The perturbation is generated only by the main process
  if (pid() == 0){
    // Initialize the spectrum
    init_2D_complex(data, NX, NY, kmin, kmax, eta0_target=amplitude);
    save_data_for_gnuplot_complex(data, NX, "initial_spectra.dat");

    // Perform the FFT2D 
    fft2D(data, NX, NX);
    save_data_for_gnuplot_complex(data, NX, "final_deformation.dat");

    // Save the results into a 2D array
    for (int i = 0; i < NX; i++){
      for (int j = 0; j < NY; j++){
        int index = i * NX + j;
        zdata[index] = data[2 * index];
      }
    }
    save_data_for_gnuplot_real(zdata, NX, "final_deformation2.dat");
  }

  // and broadcasted to the other processes if MPI
  @ if _MPI
    MPI_Bcast(zdata, NX * NY, MPI_DOUBLE, 0, MPI_COMM_WORLD);
  @endif

  // Now, we'll interpolate the perturbation into the mesh.
  gsl_interp2d *interp = gsl_interp2d_alloc(gsl_interp2d_bilinear, NX, NY);
  gsl_interp_accel *x_acc = gsl_interp_accel_alloc();
  gsl_interp_accel *y_acc = gsl_interp_accel_alloc();

  // Initialize the interpolation object
  gsl_interp2d_init(interp, xdata, ydata, zdata, NX, NY);

Apply initial condition to the scalar field. Here, we take care to normalize the perturbation using the standard deviation and multiply it by some amplitude. Also, we may apply the perturbation directly (isvof=0) to a field or use it to generate a VOF surface (isvof=1)

  if (isvof) {
    foreach_vertex()
      phi[] = gsl_interp2d_eval(interp, xdata, ydata, zdata, x, y, x_acc, y_acc) - z;
  }
  else {
    foreach(){
      phi[] = gsl_interp2d_eval(interp, xdata, ydata, zdata, x, y, x_acc, y_acc);
    }
  }  

  // Release interpolation objects 
  gsl_interp2d_free(interp);
  gsl_interp_accel_free(x_acc);
  gsl_interp_accel_free(y_acc);

  // Free Dynamically Allocated Memory
  free(xdata);
  free(ydata);
  free(zdata);
  free(data);
}

References

[thevenin2024]

Sébastien Thévenin, B-J Gréa, Gilles Kluth, and Balu Nadiga. The memory of rayleigh-taylor turbulence. arXiv preprint arXiv:2403.17832, 2024.

[dimonte2004]

Guy Dimonte, D. L. Youngs, A. Dimits, S. Weber, M. Marinak, S. Wunsch, C. Garasi, A. Robinson, M. J. Andrews, P. Ramaprabhu, A. C. Calder, B. Fryxell, J. Biello, L. Dursi, P. MacNeice, K. Olson, P. Ricker, R. Rosner, F. Timmes, H. Tufo, Y.-N. Young, and M. Zingale. A comparative study of the turbulent rayleigh–taylor instability using high-resolution three-dimensional numerical simulations: The alpha-group collaboration. Physics of Fluids, 16(5):1668–1693, 05 2004. [ DOI ]