sandbox/aberny/csgBool.c
How to use Boolean operations for geometric construction
This technique is called Constructive Solid Geometry.
#include "grid/octree.h"
#include "utils.h"
#include "fractions.h"
#include "view.h"
#include "output_stl.h"Definition of the Boolean operations
Between 2 volumes (or surfaces in 2D), we can define union, intersection and substraction operations.
Given A and B, two volumes, such that A = f(x,y,z) and B = g(x,y,z) we then have: \displaystyle A \cap B = \text{max} (f(x,y,z), g(x,y,z)) \displaystyle A \cup B = \text{min} (f(x,y,z), g(x,y,z)) \displaystyle A - B = \text{max}(f(x,y,z), -g(x,y,z)) Note that f and g must be smooth/differentiable functions. For example, a sphere can be defined using: \displaystyle f(x,y,z) = (x - x_c)^2 + (y-y_c)^2 + (z-z_c)^2 - R^2 f is negative inside the sphere, zero on the surface of the sphere and positive outside. The function is smooth everywhere.
Definition of the elementary shapes
We define two basic surfaces, a sphere and a cube.
The cube is centered on “center”, and has a length of “size”.
double cubeF (double x, double y, double z, coord center, double size)
{Our cube is defined as the intersection of 6 orthogonal planes. We define the first two planes, P1_{Plus} and P1_{Minus}.
We then define P1 has: \displaystyle P1 = P1_{Plus}\cap -P1_{Minus}
double P1_Plus = x - size/2. + center.x;
double P1_Minus = x + size/2. + center.x;
double P1 = max (P1_Plus, -P1_Minus);We apply the same process to otain P2 and P3.
double P2_Plus = y - size/2. + center.y;
double P2_Minus = y + size/2. + center.y;
double P2 = max (P2_Plus, -P2_Minus);
double P3_Plus = z - size/2. + center.z;
double P3_Minus = z + size/2. + center.z;
double P3 = max (P3_Plus, -P3_Minus);The cube is finally given by:
\displaystyle P1 \cap P2 \cap P3
double c = max (P1, max (P2, P3));
return c;
}The sphere function defines a sphere, centered on “center” and of radius “radius”.
double sphere (double x, double y, double z, coord center, double radius)
{
return (sq(x - center.x) + sq (y - center.y) + sq (z - center.z)
- sq (radius));
}
CSG operations tree.
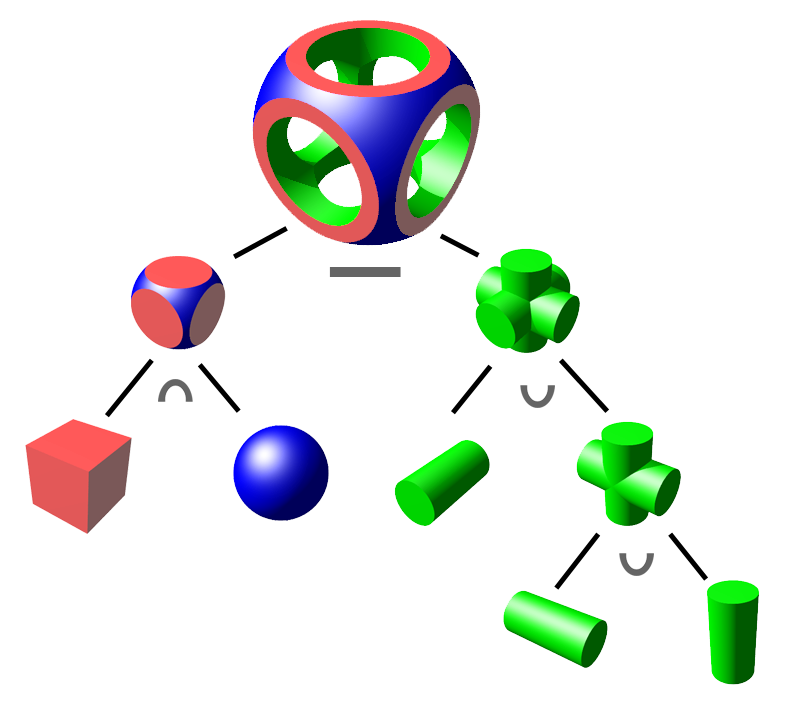
We will generate the CSG geometry example illustrated on the figure above. This geometry is defined using a cube (C); a sphere (S) and three cylinders oriented allong x, y and z (respectively X, Y and Z).
\displaystyle (C \cap S) - (X \cup Y \cup Z)
double geometry (double x, double y, double z)
{
coord center = {0,0,0};We define the sphere and the cube.
sIc is the intersection between the sphere and the cube.
double sIc = max (s, c);We define the three cylinders aligned along the x, y and z axis.
double cylinder1 = sq(x) + sq(y) - sq(0.12);
double cylinder2 = sq(z) + sq(y) - sq(0.12);
double cylinder3 = sq(x) + sq(z) - sq(0.12);We use an intermediate object for the union (to decompose the process).
double cylinderInter = min (cylinder1, cylinder2);
double cylinderUnion = min (cylinderInter, cylinder3);The final geometry is given by
return max(sIc, -cylinderUnion);
}This geometry definition can now be used to create the volumetric mesh and corresponding surface.
int main() {We shift the origin so that the simulation domain is centered on (0,0,0).
size (1 [0]);
origin (-0.5, -0.5, -0.5);We initialise the grid with 7 levels.
init_grid (1<<7);We alllocate the volume fraction field which will contain the geometry.
scalar f[];We iteratively refine the mesh around the geometry.
int iteration = 0;
do
fraction (f, geometry (x, y, z));
while (adapt_wavelet({f}, (double []){0.2}, maxlevel = 9, 2).nf &&
iteration++ <= 10);The surface can be displayed using bview.
Reconstructed VOF surface.
view (fov = 13.0359, quat = {-0.353553,0.353553,0.146447,0.853553},
bg = {1,1,1}, width = 600, height = 600);
draw_vof ("f");
draw_vof ("f", edges = true);
save ("vof.png");
stl_output_binary (f, "csg.stl");
}