houle.c

Linearized Airy Wave Theory
Code
Run
Results
Bibliography

Linearized Airy Wave Theory

We solve by Navier Stokes the small perturbation of a free surface.

The linear perturbation of interface \eta = \eta_0 e^{i(kx-\omega t)} so that \displaystyle u= \frac{k g}{\omega} \eta \cosh(ky)/cosh(kH ), \;\; v= -i \frac{k g}{\omega} \eta \sinh(ky)/cosh(kH ), \;\; P = \rho g \eta \cosh(ky)/cosh(kH ) at the surface: v= \partial \eta / \partial t= (\partial P/ \partial t) /( \rho g) hence we have the famous dispersion relation: \displaystyle \omega^2=g k \tanh(k H )

set arrow from 4,0 to 4,1 front
set arrow from 4,1 to 4,0 front
set arrow from 0.1,.1 to 9.9,0.1 front
set arrow from 9.1,.1 to 0.1,0.1 front
set label  "L0" at 6,.15 front
set label  "depth H" at 4.2,.5 front
set label  "water" at 1.2,.9 front
set label  "air" at 1.2,1.05 front
set xlabel "x"
set ylabel "h"
p [0:10]0 not,1+0.075*(cos(2*pi*x/5)+0.22121*cos(4*pi*x/5)) w filledcurves x1 linec 3 t'free surface'

periodic configuration (script)

Code

//#include "grid/multigrid.h"
#include "navier-stokes/centered.h"
#include "vof.h"
#define RHOF 1e-2
#define MU 1./10000.
// 9 ?
#define LEVEL 8
#define H 1.
#define G 1.
#define k 2.*pi/(L0/2)
#define A 0.005*H
#define w sqrt(G*k*tanh(k*H))
#define T 2*pi/w


scalar f[],*interfaces = {f};

face vector alphav[];
face vector muv[];


int main() {
    L0 = 10.;
//    N = 1 << LEVEL;
     DT = 1e-2;
    init_grid (1 << LEVEL);
    periodic (right);
 
    run();  
}

The first order terms are in cos((kx-\omega t)), The second order terms are in cos(2*(kx-\omega t)),

note: (\cosh (2 k)+2) \coth (k) \text{csch}^2(k)=\left(3-\tanh ^2(k)\right) \coth ^3(k)

event init (t = 0) {
    mask (y >  L0/4 ? top :
          none);
    const face vector g[] = {0,-G};
    a = g;
    alpha = alphav;
    scalar phi[];
    foreach_vertex(){
    double phase = k*x - w*t;
    double eta1 =  (A*cos(phase));            
    double eta2 =  pi*(A*2.)*(A*2.)*cosh(k*H)*(2.+cosh(2.*k*H))*cos(2.*phase)/(8.*(2.*pi/k)*pow(sinh(k*H),3.)); 
      phi[] = ( - y + H + eta1 + eta2) ;}
    fractions (phi, f);
    
    foreach(){
    	double phase = k*x - w*t;
        double u1 =  A*w*(cosh(k*y)/sinh(k*H))*cos(phase) ;
        double s1 = pi*(A*2.)/(2.*pi/w);
        double s2 = pi*(A*2.)/(2.*pi/k);      
        double u2 =  0.75*s1*s2*cosh(2.*k*y)*cos(2.*phase)/pow(sinh(k*H),4.); 
        double v1 = pi*(A*2.*sin(phase))*sinh(k*y)/((2.*pi/w)*sinh(k*H));
        double v2 = 0.75*s1*s2*sinh(2.*k*y)*sin(2.*phase)/pow(sinh(k*H),4.);
    	
        u.x[] =    f[] * (u1 + u2);
        u.y[] =    f[] * (v1 + v2);     
    }
}

total density

#define rho(f) ((f) + RHOF*(1. - (f)))
#define muc(f) ((f)*MU + MU/10.*(1. - (f)))


event properties (i++) {

We set a constant ad hoc viscosity field, and ad hoc density

//  const face vector muv[] = {MU,MU};
  mu = muv;
  	
    foreach_face() {
        double fm = (f[] + f[-1])/2.;
        alphav.x[] = 1./rho(fm);
        muv.x[] = muc(fm);
    }
    boundary ((scalar *){muv,alphav});
}

convergence outputs

void mg_print (mgstats mg)
{
    if (mg.i > 0 && mg.resa > 0.)
        fprintf (stderr, "#   %d %g %g %g\n", mg.i, mg.resb, mg.resa,
                 exp (log (mg.resb/mg.resa)/mg.i));
}

convergence outputs

event logfile (i++) {
    stats s = statsf (f);
    fprintf (stderr, "%g %d dt=%g %g %g %g\n", t, i, dt, s.sum, s.min, s.max - 1.);
    mg_print (mgp);
    mg_print (mgpf);
    mg_print (mgu);
    fflush (stderr);
}

for plots

event interface (t +=T;t <= 4*T){
     output_facets (f);
    fprintf(stdout,"\n");
    
    double NL=pi*(2.)*(A*2.)*cosh(k*H)*(2.+cosh(2.*k*H))/(8.*(2.*pi/k)*pow(sinh(k*H),3.));
    fprintf(stderr,"------~~~~~~-----kH=%lf period = %lf Urshell=%lf NL=%lf um=%lf,  1+%lf*(cos(%lf*x)+%lf*cos(2*%lf*x)) \n",
    k*H,T,(A*2.)/pow(2.*pi/k,3)/H,NL, A*w*(cosh(k*H)/sinh(k*H)),A,k,NL,k);

}

event movie (t += 0.05) {
    scalar l[];
    foreach()
    l[] = f[]* (   sqrt(sq(u.x[]) + sq(u.y[])));
    boundary ({l});
    static FILE * fp2 = popen ("ppm2mpeg > houle.mpg", "w");
    output_ppm (l, fp2 , min = 0,  max= A*w*(cosh(k*H)/sinh(k*H)),
      linear = true,
                n = 1024, box = {{0,-1},{10,2.5}}
                );   
    output_ppm (l, file = "houle.mp4", min = 0,  max= A*w*(cosh(k*H)/sinh(k*H)),
      linear = true,
                n = 1024, box = {{0,-1},{10,2.5}}
                );                      
    
    foreach()
    l[] = level;
    boundary ({l});
    static FILE * fp1 = popen ("ppm2mpeg > level.mpg", "w");
    output_ppm (l, fp1,   box = {{0,0},{10,2.5}})  ;            
}
event pictures (t=0.05) {
    scalar l[];
    foreach()
    l[] = f[]* (   sqrt(sq(u.x[]) + sq(u.y[])));; 
    boundary ({l});
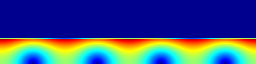
     output_ppm (l, file = "houle.png", min = 0,   max= A*w*(cosh(k*H)/sinh(k*H)),
     // linear = true,
                //n = 1024 ,
                 box = {{0,0},{10,2.5}}
                );
    foreach()
    l[] = level; 
    boundary ({l});
     output_ppm (l, file = "level.png", min = 0,   max= 12,
     // linear = true,
                //n = 1024 ,
                 box = {{0,0},{10,2.5}}
                );
             
}

event adapt(i++){
 scalar g[];
 foreach()
   g[]=f[]*noise();
 boundary({g});
 //adapt_wavelet ({g,f,u.x,u.y}, (double[]){0.01,.01,0.01,0.01}, LEVEL, 4);
 //adapt_wavelet({g,f},(double[]){0.001,0.01},maxlevel = LEVEL);
}

Run

to run

 qcc -g -O2 -Wall  -o houle houle.c -lm
 houle > out

or with makefile

make houle.tst;make houle/plots;make houle.c.html

Results

Plot of the interface

reset
set xlabel "x"
set ylabel "h(x,t=n*T)"
p[][ ]'out' w l,  1+0.005000*(cos(1.256637*x)+0.014747*cos(2*1.256637*x))  t'Stokes'

plot every period (script)

Animation of velocity

Animation velocity (click on image for animation)

Animation level (click on image for animation)

Paris 02/16

sandbox/M1EMN/Exemples/houle.c

Linearized Airy Wave Theory

Code

Run

Results

Bibliography