sandbox/Antoonvh/smokey_puff.c

A photo of a vortex ring. Image courtesy of Giesbert Nijhuis

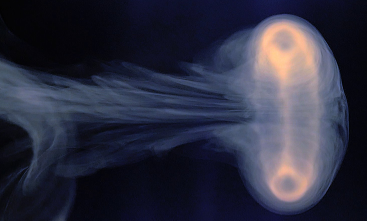
The Dispersion of a Short-Lived Turbulent Jet

Inspired by the results from the lab setup of Giesbert Nijhuis (Watch the video on Youtube), we simulate the flow resulting from a short puff of smokey air from a circular orifice. A Large Eddy Simulation (LES) formulation is used.

Setup

For this 3D case we solve the spatially-filtered version of the Navier-Stokes equations. With an eddy-viscosity closure. These are similar enough to the unfiltered equations that basically we do not need to take special care with respect to the solver. The LES extension consists mainly of a dynamic formulation of the diffusivities.

#include "grid/octree.h"
#include "navier-stokes/centered.h"
#include "SGS.h"
#include "lambda2.h"

With the duration of the ‘puff’ ti, orifice diameter R and inflow velovicity U, a dimensionless number can be identified as: \Pi=\frac{t_iU}{R}. We choose \Pi=50.

int maxlevel = 8;
double uemax = 0.02;
double  ti=50.; //We use a normalized inflow velocity and orifice diameter. 
scalar f0[], l2[];
scalar * tracers = {f0};

Relevant boundary conditions are set here.

u.n[left]  = dirichlet(1*(1+(0.001*noise()))*(sq(1) - sq(y) - sq(z)>0)*(t<=ti)); //<- This is the jet itself
f0[left]  = dirichlet((sq(1) - sq(y) - sq(z)>0)*(t<=ti)); 
u.n[right] = neumann(0);
p[right]=dirichlet(0);
Evis[left]=dirichlet(molvis); //No slip wall -> no effective eddy viscosity.

The rest is relatively straight forward stuff

int main (){
  init_grid (64);
  L0=100.;
  origin (0., -L0/2., -L0/2.);
  run();
}

event init (t = 0.){
  f0.gradient=minmod2;
  molvis=1./1000.;
  DT=1e-6; //Small time step
  TOLERANCE=1e-6; //Small Tolerance
  refine (x < 5. && sq(y) + sq(z) < sq(10.) && level < (maxlevel-1));
  refine (x < 0.1 && sq(y) + sq(z) < 2.*sq(1.) && level < (maxlevel));
  foreach(){
    f0[]=(sq(1.) - sq(y) - sq(z)-x>0.);
  }
  boundary (all);
}

event gfsview (t += ti/25.;t<=ti*10.){
  lambda2(u,l2);
  static FILE * fp =
    popen ("gfsview-batch3D smokey_puff.3djet.gfv | ppm2gif > jet3dLES.gif", "w");
  output_gfs (fp, list = {u,l2});
  fprintf (fp, "Save stdout { format = PPM width = 900 height = 600}\n");
  static FILE * fp1 =
    popen ("gfsview-batch3D smokey_puff.3djettracer.gfv | ppm2gif > tracerjetLES.gif", "w");
  output_gfs (fp1, list = {f0});
  fprintf(fp1, "Save stdout { format = PPM width = 600 height = 900}\n");
}

event adapt (i++){
  adapt_wavelet ((scalar*){u,f0}, (double[]){uemax,uemax,uemax,0.1}, maxlevel,3);

Since the initial conditions are not consistent with the boundary conditions, we start with a small timestep and tolerance for the Poisson solver. As the similuation progresses, we relax back to the default values.

  if (i<100)
    DT=DT*1.1;
  if (i==100){
    TOLERANCE=1e-3;
    DT=ti; //Switch to CFL limited timestep
  }
}

Results

One may do a visual inspection of the results:

\lambda_2 Iso-surface, coloured with colour

We see an vortex ring, a similar result as was found in the lab.

The smoke concentration field on a cross section of the puff

The smoke seems to disperse away out of the plane. Also the vortex ring seems to entrain some of the smoke far away from its source.

As an additional extra, a movie was generated in paraview that shows a volumetric rendering of the plume under different persectives. This simulation was carried out with a increased resoltion.

Web link

Giesbert Nijhuis’ website: www.laesieworks.com/