hoek.c

Hoek’s Vortex-ring generator
- Output

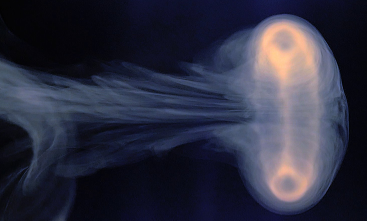
A ring vortex. Image courtesy of Giesbert Nijhuis

Hoek’s Vortex-ring generator

Rather than forcing a fluid though a circular opening, Bart Hoek proposed to force an opening though a fluid in order to generate a ring vortex. On this page we study this idea using the Navier-Stokes solver with the axisymmetric approximation.

#include "axi.h"
#include "navier-stokes/centered.h"
#include "fractions.h"
#include "view.h"
#include "particles.h"

The setup consist of a flat, circular plate (Radius Ro) with a circular opening (radius Ri) that moves for a time tc with a characteristic velocity U1.

#define U_V (2*U1*(t < tc)*sin(t*pi/tc))
#define PLATE (w - (fabs(x - xp)) - (y > Ro) - (y < Ri))
scalar plt[];

double tc = 1;   //Moving time
double w = 0.1;  //plate width
double U1 = -1;  //Plate velocity
double Ri = 1;   //Opening radius
double Ro = 5;   //The plate radius
double xp = -3;  //The plate's initial position

The domain is 30Ri $$ 30Ri.

int main(){
  L0 = 30;
  X0 = -L0/2;
  init_grid(1 << 7);
  run();
}

The setup is seeded with tracer particles, they are placed close to the opening, within a disk or radius and depth 1.5\timesRi. Furthermore, we tell the adaptation algorithm that the plate is described by a volume fraction field.

event init(t = 0){
  init_particles_2D_square_grid(60, xp - 1, 1.51, 1.5);
  int j = 0;
  while (j < n_part)
    loc[j++].z = noise()*pi;
  plt.prolongation = plt.refine = fraction_refine;
}

The plate moves and enforces a velocity via `Stephane’s trick’.

event moving_plate(i++){
  xp += dt*U_V;
  fraction(plt, PLATE);
  foreach(){
    u.y[] *= (1-plt[]);
    u.x[] = u.x[]*(1 - plt[]) + plt[]*U_V;
  }
}

event adapt(i++)
  adapt_wavelet({plt, u.x, u.y}, (double[]){0.005, 0.05, 0.05}, 10);

Output

We output a movie of the resulting flow. It displays:

A slice of the moving plate as a light gray box (upper half).
The vorticity field (upper half)
The used grid (lower half)
3600 particles that trace the flow.

Remember that the flow is two-dimensional (u = u(z,r))

Two vortex ring emerge!

For the movie we need to use a modified version of the scatter() function to visualize the axisymmetric vortex ring.

// This is copied from draw.h

redefinition of ‘glvertex3d’

static void glvertex3d (bview * view, double x, double y, double z) { 
  if (view->map) {
    coord p = {x, y, z};
    view->map (&p);
    glVertex3d (p.x, p.y, p.z);
  }
  else
    glVertex3d (x, y, z);
}

struct _scatter {
  coord * loc;    // Coordinates
  float s, pc[3], coefs[3]; // point size, colour and distance attenuation coefs.
};

void glPointParameterfv (GLenum pname, const GLfloat * params); //function protopyte

obsolete optional/named arguments syntax

trace
void scatter3Din2D(struct _scatter p){// Modified from scatter.h
  bview * view = draw();
  if (!p.coefs[0]){ // A guess:
    p.coefs[0] = 0.01;
    p.coefs[1] = 0.2;
    p.coefs[2] = 0.5;
  }

‘GL_POINT_DISTANCE_ATTENUATION’ undeclared (first use in this function)

  glPointParameterfv(GL_POINT_DISTANCE_ATTENUATION, p.coefs);

the comparison will always evaluate as ‘true’ for the address of ‘pc’ will never be NULL [-Waddress]

  if (p.pc)
    glColor3f(p.pc[0], p.pc[1], p.pc[2]);
  if (!p.s)
    p.s = 20;
  glPointSize(p.s);
  glBegin (GL_POINTS);
  for (int j = 0; j < n_part; j++)
    glvertex3d (view, p.loc[j].x, p.loc[j].y*cos(loc[j].z), p.loc[j].y*sin(loc[j].z));
  glEnd();
  view->ni++; 
}

This is the movie-making event.

event mov (t += 0.0125){
  scalar omega[];
  vorticity (u, omega);
  view (fov = 8, theta = -.75, tx = 0.05, width = 900, samples = 1);
  double std = statsf (omega).stddev;
  foreach(){
    if (fabs(omega[])*2 < std || plt[] > 0.5)
      omega[] = nodata; //Transparant
  }
  clear();
  squares ("omega", map = cool_warm, min = -6*std, max = 6*std);
  draw_vof ("plt", lw = 2);
  draw_vof ("plt", filled = 1, fc = {0.7,0.7,0.7});  
  scatter3Din2D (loc, s = 6, pc = {0.2,0.2,0.2});
  mirror ({0,-1})
    cells();
  save ("movie.mp4");
}
  
event stop (t = 6);