/**
[ ](bannerREADME.c)
# My Sandbox
Welcome to the `README` of my sandbox. This page aims to
provide an overview of the projects under [/sandbox/Antoonvh/](). The topics here reflect my interest in fluid-flow phenomena, numerical methods, popular maths and (Basilisk-)programming exercises. I hope you find something that sparks your interest.
-*Antoon van Hooft*-
## Physical Systems
#### Atmospheric Flows
[
](bannerREADME.c)
# My Sandbox
Welcome to the `README` of my sandbox. This page aims to
provide an overview of the projects under [/sandbox/Antoonvh/](). The topics here reflect my interest in fluid-flow phenomena, numerical methods, popular maths and (Basilisk-)programming exercises. I hope you find something that sparks your interest.
-*Antoon van Hooft*-
## Physical Systems
#### Atmospheric Flows
[ ](lee.c)
* [An Adaptive Single-Column Model for the Stable Atmospheric Boundary Layer](GABLS1.c)
* [Growth and decay of Convection into a Stratified Fluid over a Warm Surface](vhm16.c)
* [Atmospheric waves induced by a mountain](lee.c)
* [Shallow cumulus convection](bomex.c)
* [A rising moist bubble](moist_bubble.c)
* [A convective boundary layer on a small planet](convection_cyl.c)
* [A section of a subsiding shell](subsiding-shell.c)
* [The diurnal cycle of the atmosphere](lumpedrob.c)
#### 3D Turbulence
[
](lee.c)
* [An Adaptive Single-Column Model for the Stable Atmospheric Boundary Layer](GABLS1.c)
* [Growth and decay of Convection into a Stratified Fluid over a Warm Surface](vhm16.c)
* [Atmospheric waves induced by a mountain](lee.c)
* [Shallow cumulus convection](bomex.c)
* [A rising moist bubble](moist_bubble.c)
* [A convective boundary layer on a small planet](convection_cyl.c)
* [A section of a subsiding shell](subsiding-shell.c)
* [The diurnal cycle of the atmosphere](lumpedrob.c)
#### 3D Turbulence
[ ](two_rings.c)
* [LES of a Vortex Cannon](smokey_puff.c)
* [LES of Isotropic Turbulence in a Triply Periodic Box](isotropicLES.c)
* [A Kelvin-Helmholtz instability in 3D](kh3d.c)
* [The collision of two vortex rings](two_rings.c)
* [Untying a vortex knot](trefoil4.c)
#### 2D Turbulence and Vortex Dynamics
[
](two_rings.c)
* [LES of a Vortex Cannon](smokey_puff.c)
* [LES of Isotropic Turbulence in a Triply Periodic Box](isotropicLES.c)
* [A Kelvin-Helmholtz instability in 3D](kh3d.c)
* [The collision of two vortex rings](two_rings.c)
* [Untying a vortex knot](trefoil4.c)
#### 2D Turbulence and Vortex Dynamics
[ ](lamb-dipole.c)
* [Hoek's Ring-Vortex Generator](hoek.c)
* [The Collision of a Dipolar Vortex with a No-slip Wall](lamb-dipole.c)
* [The Structure of Dipolar Vortices](wong2015.c)
* [A Kelvin-Helmholtz instability in 2D](kh.c)
* [A Rayleigh-Taylor instability](rt.c)
* [Vortex rebound from an opening](rebound2.c)
* [Unstable flow around a Cylinder](kizner2.c)
#### Multiphase flows
[
](lamb-dipole.c)
* [Hoek's Ring-Vortex Generator](hoek.c)
* [The Collision of a Dipolar Vortex with a No-slip Wall](lamb-dipole.c)
* [The Structure of Dipolar Vortices](wong2015.c)
* [A Kelvin-Helmholtz instability in 2D](kh.c)
* [A Rayleigh-Taylor instability](rt.c)
* [Vortex rebound from an opening](rebound2.c)
* [Unstable flow around a Cylinder](kizner2.c)
#### Multiphase flows
[ ](rest.c)
* [Four Droples in two binary Collisions](coalescence.c)
* [Droplet splashes in a Pool](splash.c)
* [The descent of Rain Droplets](rain.c)
* [Liquid Planets and their Gravity Field](gravity.c)
* [A 2D Bouncing Droplet in Space](bounce.c)
* [An Axisymmetric Bouncing Droplet in Space](axibounce.c)
* [Droplets resting on a hydrophobic material](rest.c)
* [A bathtub vortex](bathtub.c)
* [A plant's capillary](cap.c)
* [A Droplet water slide](dws.c)
#### Other
[
](rest.c)
* [Four Droples in two binary Collisions](coalescence.c)
* [Droplet splashes in a Pool](splash.c)
* [The descent of Rain Droplets](rain.c)
* [Liquid Planets and their Gravity Field](gravity.c)
* [A 2D Bouncing Droplet in Space](bounce.c)
* [An Axisymmetric Bouncing Droplet in Space](axibounce.c)
* [Droplets resting on a hydrophobic material](rest.c)
* [A bathtub vortex](bathtub.c)
* [A plant's capillary](cap.c)
* [A Droplet water slide](dws.c)
#### Other
[ ](tesla_valve.c)
* [Mixing Milk into Coffee](coffee.c)
* [Internal Waves and the Dispersion Relation](internalwacesMG.c)
* [Flow over a stress-free mountain (test)](embed-freeslip.c)
* [Laminar mixing of paint](laminarmixing.c)
* [Flow in a toroidal geometry](tube.c)
* [A particle-driven flow](ash.c)
* [Liquid core convection](core.c)
* [Tesla's valve](tesla_valve.c)
* [Scalar mixing front in a tube flow](pois-front.c)
## Maths
[
](tesla_valve.c)
* [Mixing Milk into Coffee](coffee.c)
* [Internal Waves and the Dispersion Relation](internalwacesMG.c)
* [Flow over a stress-free mountain (test)](embed-freeslip.c)
* [Laminar mixing of paint](laminarmixing.c)
* [Flow in a toroidal geometry](tube.c)
* [A particle-driven flow](ash.c)
* [Liquid core convection](core.c)
* [Tesla's valve](tesla_valve.c)
* [Scalar mixing front in a tube flow](pois-front.c)
## Maths
[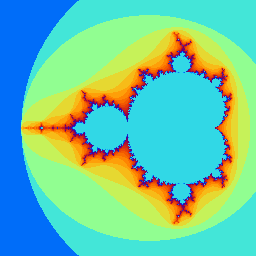 ](mandelbrot2.c)
* [Root Finding of an Analytical Function using an Adaptive Grid](root-finding.c)
* [The Fractal Dimension of the Koch Snowflake](koch.c)
* [An example of a shape with a scale-dependent fractal dimension](coil.c)
* Visualization of the Mandelbrot set
a. [A zoom in on a specific location](mandelbrot.c)
b. [A high resolution image of the entire set](mandelbrot2.c)
* The distribution of the prime numbers along a Z-order space-filling curve:
a. [In two dimensions](primes.c)
b. [In three dimensions](primes3D.c)
* [The locality of a Z-index curve and a regular Cartesian-style curve](mortcscart.c)
* [A Hilbert curve grid iterator](hilbert.c)
* [Solitary Solutions for the Korteweg-De Vries Equation](KdV.c)
* [Solving an implicit integral equation](ti2.c)
* [The Helmholtz filter](hf.c)
## Methods
[
](mandelbrot2.c)
* [Root Finding of an Analytical Function using an Adaptive Grid](root-finding.c)
* [The Fractal Dimension of the Koch Snowflake](koch.c)
* [An example of a shape with a scale-dependent fractal dimension](coil.c)
* Visualization of the Mandelbrot set
a. [A zoom in on a specific location](mandelbrot.c)
b. [A high resolution image of the entire set](mandelbrot2.c)
* The distribution of the prime numbers along a Z-order space-filling curve:
a. [In two dimensions](primes.c)
b. [In three dimensions](primes3D.c)
* [The locality of a Z-index curve and a regular Cartesian-style curve](mortcscart.c)
* [A Hilbert curve grid iterator](hilbert.c)
* [Solitary Solutions for the Korteweg-De Vries Equation](KdV.c)
* [Solving an implicit integral equation](ti2.c)
* [The Helmholtz filter](hf.c)
## Methods
[ ](profile5c.h)
* [A Header file for the Implementation of an Eddy Viscosity Closure](SGS.h)
* [The Vreman Eddy Viscosity model](vreman.h)
* [A function that finds the location and size of the(/a) critical CFL-limited-timestep cell](criticallocation.h)
* [Law of the wall for flows over a rough (`bottom`) surface](law-of-the-wall.h)
* [Read $x-y-z$ formatted binary data](readxyz.h)
* [Draw isolines in `bview3D`](iso_3D.c)
* [Reconstruct geometries](reconstruct.h)
* [Distance to volume fraction fields](frac-dist.h)
* [Higher-order methods and definitions](higher-order.h)
* Solution diagnostics
a. [A vertical-averaging profiling function](profile5c.h)
b. [A generic interface-averaging profiling function](profile6.h)
c. [Diagnose solution fields along a 2D interface](interface_iterator.h)
d. [A function that computes a second order longitudional structure function of a vector field](structure_function.h)
[
](profile5c.h)
* [A Header file for the Implementation of an Eddy Viscosity Closure](SGS.h)
* [The Vreman Eddy Viscosity model](vreman.h)
* [A function that finds the location and size of the(/a) critical CFL-limited-timestep cell](criticallocation.h)
* [Law of the wall for flows over a rough (`bottom`) surface](law-of-the-wall.h)
* [Read $x-y-z$ formatted binary data](readxyz.h)
* [Draw isolines in `bview3D`](iso_3D.c)
* [Reconstruct geometries](reconstruct.h)
* [Distance to volume fraction fields](frac-dist.h)
* [Higher-order methods and definitions](higher-order.h)
* Solution diagnostics
a. [A vertical-averaging profiling function](profile5c.h)
b. [A generic interface-averaging profiling function](profile6.h)
c. [Diagnose solution fields along a 2D interface](interface_iterator.h)
d. [A function that computes a second order longitudional structure function of a vector field](structure_function.h)
[ ](bwatch.h)
* [Generic Particle functions](particle.h)
- [Flow tracers](tracer-particles.h)
* [vof-interface-bounded tracers](vof-tracer-particles.h)
- [Inertial particles](inertial-particles.h)
* [Cosmological dynamics](cosmology.h)
* [Stokes particles](stokes-particles.h)
- [A bview function for plotting particles](scatter2.h)
* [Ray-casting visualization](bwatch.h)
* [A Robin/mixed boundary condition](robin.c)
* [5-point 8th-order accurate finite-difference derivatives](pade.c)
* [A 4th-order accurate solver for the Navier-Stokes equations](nsf4t.h)
## Documentation
I invested some time in reading the source code to get some additional
information on how the tree-grid structure is implemented in Basilisk
and how Adaptivity works. To organize my toughts I wrote it down.
* [The Tree-Grid structure in Basilisk](The_Tree-Grid_Structure_in_Basilisk)
* [The Wavelet Based Adaptive Grid Algorithm](the_adaptive_wavelet_algorithm)
## Other READMEs
* [Overview of pages used in published articles](README.pubs)
* [Tests for numerical schemes](README.conv)
* [Overview of pages for the Plantenna project](tree/README)
## Miscellaneous pages
[
](bwatch.h)
* [Generic Particle functions](particle.h)
- [Flow tracers](tracer-particles.h)
* [vof-interface-bounded tracers](vof-tracer-particles.h)
- [Inertial particles](inertial-particles.h)
* [Cosmological dynamics](cosmology.h)
* [Stokes particles](stokes-particles.h)
- [A bview function for plotting particles](scatter2.h)
* [Ray-casting visualization](bwatch.h)
* [A Robin/mixed boundary condition](robin.c)
* [5-point 8th-order accurate finite-difference derivatives](pade.c)
* [A 4th-order accurate solver for the Navier-Stokes equations](nsf4t.h)
## Documentation
I invested some time in reading the source code to get some additional
information on how the tree-grid structure is implemented in Basilisk
and how Adaptivity works. To organize my toughts I wrote it down.
* [The Tree-Grid structure in Basilisk](The_Tree-Grid_Structure_in_Basilisk)
* [The Wavelet Based Adaptive Grid Algorithm](the_adaptive_wavelet_algorithm)
## Other READMEs
* [Overview of pages used in published articles](README.pubs)
* [Tests for numerical schemes](README.conv)
* [Overview of pages for the Plantenna project](tree/README)
## Miscellaneous pages
[ ](game/README)
* [Playing games with Basilisk](game/README)
* [A cautionary note on the simulation of a sharp inversion layer](wiggelyiversionlayer.c)
* [A cautionary note on using the Navier-Stokes solver without a properly initialized/restored pressure field](afluidatrest.c)
* [A cautionary note on using surface tension in combination with grid adaptivity](bootstrapbubble.c)
* [Evaluating a line integral on a tree grid](line_integrate.c)
* Experimental adaptivity pages
a. [A (test of a) flexible wavelet-based adaptation algorithm](testadapt2.c)
b. [A space-time adaptive solver](my_second_MG_solver.c)
c. [Adaptively computing a maximum level](kramer.c)
d. [A very flexible adaption function](adapt_field.h)
e. [An adaptivite method on an equidistant grid](polynominal_adaptivity.c)
* [Encode a movie on an octree](ri.c)
* [Hilbert-order MPI-domain decomposition on trees](test_Hilbert.c)
* [Code your own flow-problem solver (external link)](https://antoonvanhooft.nl/min_ns/intro)
## Contact
If you like to discuss a specific topic, feel free to e-mail me:
j.a.v.hooft-${\mathcal{A}}$-gmail.com. I also have a [website](https://antoonvanhooft.nl).
[
](game/README)
* [Playing games with Basilisk](game/README)
* [A cautionary note on the simulation of a sharp inversion layer](wiggelyiversionlayer.c)
* [A cautionary note on using the Navier-Stokes solver without a properly initialized/restored pressure field](afluidatrest.c)
* [A cautionary note on using surface tension in combination with grid adaptivity](bootstrapbubble.c)
* [Evaluating a line integral on a tree grid](line_integrate.c)
* Experimental adaptivity pages
a. [A (test of a) flexible wavelet-based adaptation algorithm](testadapt2.c)
b. [A space-time adaptive solver](my_second_MG_solver.c)
c. [Adaptively computing a maximum level](kramer.c)
d. [A very flexible adaption function](adapt_field.h)
e. [An adaptivite method on an equidistant grid](polynominal_adaptivity.c)
* [Encode a movie on an octree](ri.c)
* [Hilbert-order MPI-domain decomposition on trees](test_Hilbert.c)
* [Code your own flow-problem solver (external link)](https://antoonvanhooft.nl/min_ns/intro)
## Contact
If you like to discuss a specific topic, feel free to e-mail me:
j.a.v.hooft-${\mathcal{A}}$-gmail.com. I also have a [website](https://antoonvanhooft.nl).
[ ](rt.c)
*/
](rt.c)
*/ ](bannerREADME.c)
# My Sandbox
Welcome to the `README` of my sandbox. This page aims to
provide an overview of the projects under [/sandbox/Antoonvh/](). The topics here reflect my interest in fluid-flow phenomena, numerical methods, popular maths and (Basilisk-)programming exercises. I hope you find something that sparks your interest.
-*Antoon van Hooft*-
## Physical Systems
#### Atmospheric Flows
[
](bannerREADME.c)
# My Sandbox
Welcome to the `README` of my sandbox. This page aims to
provide an overview of the projects under [/sandbox/Antoonvh/](). The topics here reflect my interest in fluid-flow phenomena, numerical methods, popular maths and (Basilisk-)programming exercises. I hope you find something that sparks your interest.
-*Antoon van Hooft*-
## Physical Systems
#### Atmospheric Flows
[ ](lee.c)
* [An Adaptive Single-Column Model for the Stable Atmospheric Boundary Layer](GABLS1.c)
* [Growth and decay of Convection into a Stratified Fluid over a Warm Surface](vhm16.c)
* [Atmospheric waves induced by a mountain](lee.c)
* [Shallow cumulus convection](bomex.c)
* [A rising moist bubble](moist_bubble.c)
* [A convective boundary layer on a small planet](convection_cyl.c)
* [A section of a subsiding shell](subsiding-shell.c)
* [The diurnal cycle of the atmosphere](lumpedrob.c)
#### 3D Turbulence
[
](lee.c)
* [An Adaptive Single-Column Model for the Stable Atmospheric Boundary Layer](GABLS1.c)
* [Growth and decay of Convection into a Stratified Fluid over a Warm Surface](vhm16.c)
* [Atmospheric waves induced by a mountain](lee.c)
* [Shallow cumulus convection](bomex.c)
* [A rising moist bubble](moist_bubble.c)
* [A convective boundary layer on a small planet](convection_cyl.c)
* [A section of a subsiding shell](subsiding-shell.c)
* [The diurnal cycle of the atmosphere](lumpedrob.c)
#### 3D Turbulence
[ ](two_rings.c)
* [LES of a Vortex Cannon](smokey_puff.c)
* [LES of Isotropic Turbulence in a Triply Periodic Box](isotropicLES.c)
* [A Kelvin-Helmholtz instability in 3D](kh3d.c)
* [The collision of two vortex rings](two_rings.c)
* [Untying a vortex knot](trefoil4.c)
#### 2D Turbulence and Vortex Dynamics
[
](two_rings.c)
* [LES of a Vortex Cannon](smokey_puff.c)
* [LES of Isotropic Turbulence in a Triply Periodic Box](isotropicLES.c)
* [A Kelvin-Helmholtz instability in 3D](kh3d.c)
* [The collision of two vortex rings](two_rings.c)
* [Untying a vortex knot](trefoil4.c)
#### 2D Turbulence and Vortex Dynamics
[ ](lamb-dipole.c)
* [Hoek's Ring-Vortex Generator](hoek.c)
* [The Collision of a Dipolar Vortex with a No-slip Wall](lamb-dipole.c)
* [The Structure of Dipolar Vortices](wong2015.c)
* [A Kelvin-Helmholtz instability in 2D](kh.c)
* [A Rayleigh-Taylor instability](rt.c)
* [Vortex rebound from an opening](rebound2.c)
* [Unstable flow around a Cylinder](kizner2.c)
#### Multiphase flows
[
](lamb-dipole.c)
* [Hoek's Ring-Vortex Generator](hoek.c)
* [The Collision of a Dipolar Vortex with a No-slip Wall](lamb-dipole.c)
* [The Structure of Dipolar Vortices](wong2015.c)
* [A Kelvin-Helmholtz instability in 2D](kh.c)
* [A Rayleigh-Taylor instability](rt.c)
* [Vortex rebound from an opening](rebound2.c)
* [Unstable flow around a Cylinder](kizner2.c)
#### Multiphase flows
[ ](tesla_valve.c)
* [Mixing Milk into Coffee](coffee.c)
* [Internal Waves and the Dispersion Relation](internalwacesMG.c)
* [Flow over a stress-free mountain (test)](embed-freeslip.c)
* [Laminar mixing of paint](laminarmixing.c)
* [Flow in a toroidal geometry](tube.c)
* [A particle-driven flow](ash.c)
* [Liquid core convection](core.c)
* [Tesla's valve](tesla_valve.c)
* [Scalar mixing front in a tube flow](pois-front.c)
## Maths
[
](tesla_valve.c)
* [Mixing Milk into Coffee](coffee.c)
* [Internal Waves and the Dispersion Relation](internalwacesMG.c)
* [Flow over a stress-free mountain (test)](embed-freeslip.c)
* [Laminar mixing of paint](laminarmixing.c)
* [Flow in a toroidal geometry](tube.c)
* [A particle-driven flow](ash.c)
* [Liquid core convection](core.c)
* [Tesla's valve](tesla_valve.c)
* [Scalar mixing front in a tube flow](pois-front.c)
## Maths
[ ](mandelbrot2.c)
* [Root Finding of an Analytical Function using an Adaptive Grid](root-finding.c)
* [The Fractal Dimension of the Koch Snowflake](koch.c)
* [An example of a shape with a scale-dependent fractal dimension](coil.c)
* Visualization of the Mandelbrot set
a. [A zoom in on a specific location](mandelbrot.c)
b. [A high resolution image of the entire set](mandelbrot2.c)
* The distribution of the prime numbers along a Z-order space-filling curve:
a. [In two dimensions](primes.c)
b. [In three dimensions](primes3D.c)
* [The locality of a Z-index curve and a regular Cartesian-style curve](mortcscart.c)
* [A Hilbert curve grid iterator](hilbert.c)
* [Solitary Solutions for the Korteweg-De Vries Equation](KdV.c)
* [Solving an implicit integral equation](ti2.c)
* [The Helmholtz filter](hf.c)
## Methods
[
](mandelbrot2.c)
* [Root Finding of an Analytical Function using an Adaptive Grid](root-finding.c)
* [The Fractal Dimension of the Koch Snowflake](koch.c)
* [An example of a shape with a scale-dependent fractal dimension](coil.c)
* Visualization of the Mandelbrot set
a. [A zoom in on a specific location](mandelbrot.c)
b. [A high resolution image of the entire set](mandelbrot2.c)
* The distribution of the prime numbers along a Z-order space-filling curve:
a. [In two dimensions](primes.c)
b. [In three dimensions](primes3D.c)
* [The locality of a Z-index curve and a regular Cartesian-style curve](mortcscart.c)
* [A Hilbert curve grid iterator](hilbert.c)
* [Solitary Solutions for the Korteweg-De Vries Equation](KdV.c)
* [Solving an implicit integral equation](ti2.c)
* [The Helmholtz filter](hf.c)
## Methods
[ ](bwatch.h)
* [Generic Particle functions](particle.h)
- [Flow tracers](tracer-particles.h)
* [vof-interface-bounded tracers](vof-tracer-particles.h)
- [Inertial particles](inertial-particles.h)
* [Cosmological dynamics](cosmology.h)
* [Stokes particles](stokes-particles.h)
- [A bview function for plotting particles](scatter2.h)
* [Ray-casting visualization](bwatch.h)
* [A Robin/mixed boundary condition](robin.c)
* [5-point 8th-order accurate finite-difference derivatives](pade.c)
* [A 4th-order accurate solver for the Navier-Stokes equations](nsf4t.h)
## Documentation
I invested some time in reading the source code to get some additional
information on how the tree-grid structure is implemented in Basilisk
and how Adaptivity works. To organize my toughts I wrote it down.
* [The Tree-Grid structure in Basilisk](The_Tree-Grid_Structure_in_Basilisk)
* [The Wavelet Based Adaptive Grid Algorithm](the_adaptive_wavelet_algorithm)
## Other READMEs
* [Overview of pages used in published articles](README.pubs)
* [Tests for numerical schemes](README.conv)
* [Overview of pages for the Plantenna project](tree/README)
## Miscellaneous pages
[
](bwatch.h)
* [Generic Particle functions](particle.h)
- [Flow tracers](tracer-particles.h)
* [vof-interface-bounded tracers](vof-tracer-particles.h)
- [Inertial particles](inertial-particles.h)
* [Cosmological dynamics](cosmology.h)
* [Stokes particles](stokes-particles.h)
- [A bview function for plotting particles](scatter2.h)
* [Ray-casting visualization](bwatch.h)
* [A Robin/mixed boundary condition](robin.c)
* [5-point 8th-order accurate finite-difference derivatives](pade.c)
* [A 4th-order accurate solver for the Navier-Stokes equations](nsf4t.h)
## Documentation
I invested some time in reading the source code to get some additional
information on how the tree-grid structure is implemented in Basilisk
and how Adaptivity works. To organize my toughts I wrote it down.
* [The Tree-Grid structure in Basilisk](The_Tree-Grid_Structure_in_Basilisk)
* [The Wavelet Based Adaptive Grid Algorithm](the_adaptive_wavelet_algorithm)
## Other READMEs
* [Overview of pages used in published articles](README.pubs)
* [Tests for numerical schemes](README.conv)
* [Overview of pages for the Plantenna project](tree/README)
## Miscellaneous pages
[ ](game/README)
* [Playing games with Basilisk](game/README)
* [A cautionary note on the simulation of a sharp inversion layer](wiggelyiversionlayer.c)
* [A cautionary note on using the Navier-Stokes solver without a properly initialized/restored pressure field](afluidatrest.c)
* [A cautionary note on using surface tension in combination with grid adaptivity](bootstrapbubble.c)
* [Evaluating a line integral on a tree grid](line_integrate.c)
* Experimental adaptivity pages
a. [A (test of a) flexible wavelet-based adaptation algorithm](testadapt2.c)
b. [A space-time adaptive solver](my_second_MG_solver.c)
c. [Adaptively computing a maximum level](kramer.c)
d. [A very flexible adaption function](adapt_field.h)
e. [An adaptivite method on an equidistant grid](polynominal_adaptivity.c)
* [Encode a movie on an octree](ri.c)
* [Hilbert-order MPI-domain decomposition on trees](test_Hilbert.c)
* [Code your own flow-problem solver (external link)](https://antoonvanhooft.nl/min_ns/intro)
## Contact
If you like to discuss a specific topic, feel free to e-mail me:
j.a.v.hooft-${\mathcal{A}}$-gmail.com. I also have a [website](https://antoonvanhooft.nl).
[
](game/README)
* [Playing games with Basilisk](game/README)
* [A cautionary note on the simulation of a sharp inversion layer](wiggelyiversionlayer.c)
* [A cautionary note on using the Navier-Stokes solver without a properly initialized/restored pressure field](afluidatrest.c)
* [A cautionary note on using surface tension in combination with grid adaptivity](bootstrapbubble.c)
* [Evaluating a line integral on a tree grid](line_integrate.c)
* Experimental adaptivity pages
a. [A (test of a) flexible wavelet-based adaptation algorithm](testadapt2.c)
b. [A space-time adaptive solver](my_second_MG_solver.c)
c. [Adaptively computing a maximum level](kramer.c)
d. [A very flexible adaption function](adapt_field.h)
e. [An adaptivite method on an equidistant grid](polynominal_adaptivity.c)
* [Encode a movie on an octree](ri.c)
* [Hilbert-order MPI-domain decomposition on trees](test_Hilbert.c)
* [Code your own flow-problem solver (external link)](https://antoonvanhooft.nl/min_ns/intro)
## Contact
If you like to discuss a specific topic, feel free to e-mail me:
j.a.v.hooft-${\mathcal{A}}$-gmail.com. I also have a [website](https://antoonvanhooft.nl).
[ ](rt.c)
*/
](rt.c)
*/